Правильные многогранники.
Все ребра правильного многогранника равны друг другу. Равны также все его двугранные углы, содержащие две грани с общим ребром
(для информации: Двугранный угол – это фигура, образованная двумя полуплоскостями, исходящими из одной прямой
Грани правильного многогранника могут быть либо равносторонними треугольниками, либо квадратами, либо правильными пятиугольниками. Действительно, угол правильного 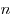 -угольника при
-угольника при  не меньше
не меньше  . С другой стороны, при каждой вершине многогранника должно быть не менее трех плоских углов. Поэтому если бы существовал правильный многогранник, у которого грани – правильные n-угольники при
. С другой стороны, при каждой вершине многогранника должно быть не менее трех плоских углов. Поэтому если бы существовал правильный многогранник, у которого грани – правильные n-угольники при  , то сумма плоских углов при каждой вершине такого многогранника была бы не меньше чем
, то сумма плоских углов при каждой вершине такого многогранника была бы не меньше чем  . Но это невозможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше
. Но это невозможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше  .
.
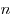 -угольника при
-угольника при  не меньше
не меньше  . С другой стороны, при каждой вершине многогранника должно быть не менее трех плоских углов. Поэтому если бы существовал правильный многогранник, у которого грани – правильные n-угольники при
. С другой стороны, при каждой вершине многогранника должно быть не менее трех плоских углов. Поэтому если бы существовал правильный многогранник, у которого грани – правильные n-угольники при  , то сумма плоских углов при каждой вершине такого многогранника была бы не меньше чем
, то сумма плоских углов при каждой вершине такого многогранника была бы не меньше чем  . Но это невозможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше
. Но это невозможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше  .
.
По этой же причине каждая вершина правильного многогранника может быть вершиной либо трех, четырех или пяти равносторонних треугольников, либо трех квадратов, либо трех правильных пятиугольников. Других возможностей нет.
Перечислим правильные многогранники:
- Правильный тетраэдр (четырехгранник) — многогранник, составленный из четырех правильных треугольников (рис.1а).
- Правильный гексаэдр (шестигранник) или куб — многогранник, составленный из шести правильных четырехугольников (квадратов) (рис. 1б).
- Правильный октаэдр (восьмигранник) — многогранник, составленный из восьми правильных треугольников (рис. 1в).
- Правильный додекаэдр (двенадцатигранник) — многогранник, составленный из двенадцати правильных пятиугольников (рис. 1г).
- Правильный икосаэдр (двадцатигранник) — многогранник, составленный из двадцати правильных треугольников (рис. 1д).
Центры граней каждого правильного многогранника являются вершинами другого правильного многогранника.
и наоборот:
Такие пары многогранников (куб и октаэдрит) называют двойственными друг другу правильными многогранниками.
Задание 1
Какие пары двойственных фигур вы еще можете назвать? (совет: прочтите параграф 9.5 учебника)
Задание 2
Задание 3
Симметрия правильный многогранников
Расскажем о симметрии правильных многогранников. Начнем с правильного
тетраэдра.
В правильном тетраэдре шесть плоскостей симметрии: каждая такая плоскость
определяется ребром тетраэдра и серединой скрещивающегося с ним ребра (рис.2.87,а).
Две плоскости симметрии тетраэдра, содержащие два его скрещивающихся ребра,
пересекаются по прямой, проходящей через середины этих скрещивающихся ребер (рис.2.87,б).
Такая прямая является осью симметрии тетраэдра. У тетраэдра три оси симметрии.
Кроме перечисленных видов симметрии, тетраэдр обладает поворотной симметрией на
угол 1200
- вокруг прямой, содержащей высоту тетраэдра (рис.2.87,в). Таких осей поворота
четыре - по числу высот тетраэдра.
Центра симметрии правильный тетраэдр не имеет. Это легко объясняется, например, тем,
что правильный тетраэдр не имеет параллельных граней.
Перейдем теперь к кубу. Куб (как и произвольный параллелепипед) имеет центр
симметрии - точку пересечения диагоналей.
Оси симметрии куба изображены на рисунке 2.88.
Те его оси симметрии куба, которые
проходят через центры его противоположных граней, являются и осями его поворотной
симметрии на угол 90
Задание 4
Могут ли изображенные на рисунке 94 многогранники быть
правильными многогранниками?
Задание 5 Учебник стр. 99 № 9.26
Задание 6
Делаем: Сделайте развертку правильного додекаэдра: вырежьте из картона два
одинаковых многоугольника, изображенных на рисунке 1а, положите их друг на друга так,
как показано на рисунке 2 б и склейте, Результат работы принести на урок!
(для информации. Развёртка многогранника — совокупность многоугольников, соответственно равных граням многогранника, с указанием того, какие стороны и вершины многоугольников соответствуют одним и тем же рёбрам и вершинам многогранника[1]. Модели многогранников часто склеиваются из развёрток или отдельных многоугольников с указанием сторон, которые должны быть склеены)
Задание 6
Задание 6
Задание 7
Д/З :1. Лекция + п 9.5 +вопросы после параграфа.
2. №9.24,9.26
3. Выполнить задания, указанные выше
4. принести развертку додекаэдра + додекаэдр (по заданию 6)
(данное д/з на 2 пропущенных урока)













Здравствуйте, вы же сказали, что скажете кому какой делать
ОтветитьУдалитьЕлена Михайловна, можно раскрасить этот додекоэдр?
ОтветитьУдалитьЕлена Михайловна, можно раскрасить этот додекоэдр?
ОтветитьУдалить